XXH3 - a new speed-optimized hash algorithm
The xxHash family of hash functions has proven more successful than anticipated. Initially designed as a checksum companion for LZ4, it has found its way into many more projects, requiring vastly different workloads.
I was recently summoned to investigate performance for a bloom filter implementation, requiring to generate quickly 64 pseudo-random bits from small inputs of variable length. XXH64 could fit the bill, but performance on small inputs, never was its priority. It’s not completely wasteful either, it pays a bit attention to short inputs thanks to a small speed module in SMHasher. However, the module itself does the bare minimum, and it was not clear to me what’s exactly measured.
So I decided to create my own benchmark program, as a way to ensure that I understand and control what’s being measured. This was a very interesting journey, leading to surprising discoveries.
The end result of this investigation is XXH3, a cross-over inspired by many other great hash algorithms, which proves substantially faster than existing variants of xxHash, across basically all dimensions.
Let’s detail those dimensions, and give some credit where inspiration is due.
Checksumming long inputs
xxHash started as a fast checksum for LZ4, and I believe it can still be useful for this purpose. It has proven popular among movie makers for file transfer verification, saving a lot of time thanks to its great speed. The main downside is that XXH64() is limited to 64-bit, which is insufficient when comparing a really large number of files (and by large I mean many many million ones). For this reason, a 128-bit variant has often been requested,
XXH3 features a wide internal state of 512 bits, which makes it suitable to generate a hash of up to 256 bit. For the time being, only 64-bit and 128-bit variants are exposed, but a similar recipe can be used for a 256-bit variant if there is any need for it one day. All variant feature same speed, since only the finalization stage is different.
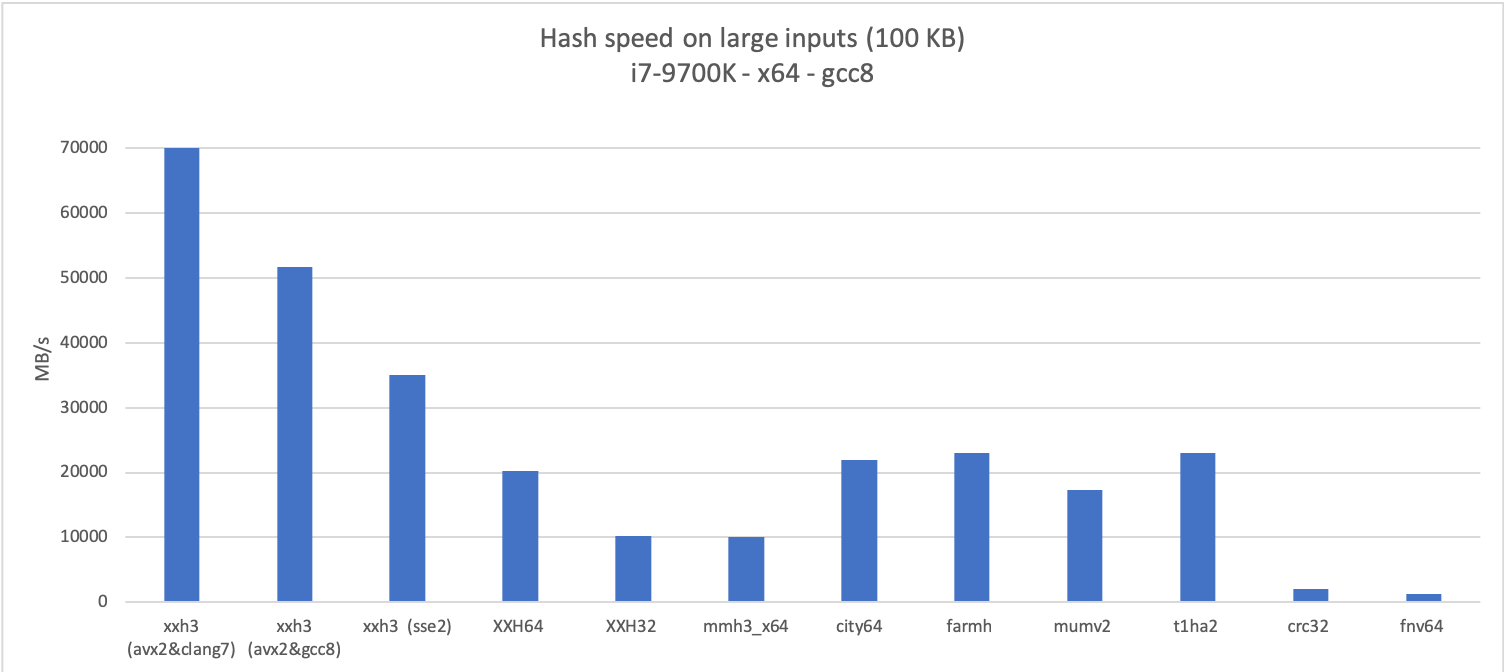
I’m using this opportunity to compare with a few other well known hash algorithms, either because their notoriety makes them frequently named in discussions related to hash algorithms (FNV, CRC), or because they are very good in at least one dimension.
XXH3 proves very fast on large inputs, thanks to a vector-friendly inner-loop, inspired Bulat Ziganshin’s Farsh, itself based on UMAC paper.
Unfortunately, UMAC features a critical flaw for checksumming, which makes it ignore 4 bytes of input, on average every 16 GB. This might not seem much, and it might even be acceptable if the goal is to generate a 32-bit checksum as in the original paper. But for checksumming large files with 64-bit or 128-bit fingerprints, this is a big no-no.
So the version embedded into XXH3 is modified, to guarantee that all input bytes are necessarily present in the final mix. This makes it a bit slower, but as can be seen in the graphs, it remains plenty fast.
Vectorization must be done manually, using intrinsic, as the compiler seems unable to properly auto-vectorize the scalar code path.
For this reason, the code offers 4 paths : scalar (universal), SSE2, AVX2, and also NEON offered by Devin Hussey. It may be possible to vectorize additional platforms, though this requires dedicated efforts.
SSE2 is enough to reach substantial speed, which is great because all x64 cpus necessarily support this instruction set. SSE2 is also free of dynamic throttling issues, and is automatically enabled on all x64 compilers. Hence I expect it to be the most common target.
On a given code path, compilers can make a difference. For example, AVX2 vectorization is significantly more effective with clang. Actually, the speed of this variant is so fast that I was wondering if it was faster than my main memory. So I graphed the speed over a variety of input sizes.

As one can see, the AVX2 build is much faster than main memory, and the impact of cache size is now clearly observable, at 32 KB (L1), 256 KB (L2) and 8 MB (L3). As a rule, “top speed” is only achievable when data is already in cache.
So is it worth being so fast ?
If data is very large (say, a movie), it can’t fit in the cache, so the bottleneck will be at best the main memory, if not I/O system itself. In which case, a faster hash may save cpu time, but will not make the checksumming operation faster.
On the other hand, there are many use cases where data is neither large nor small, say in the KB range. This includes many types of record, typical of database workloads. In these use cases, hashing is not the main operation : it’s just one of many operations, sandwiched between other pieces of code. Input data is already in the cache, because it was needed anyway by these other operations. In such a scenario, hashing faster helps to a faster overall run time, as cpu savings are employed by subsequent operations.
32-bit friendliness
The computing world is massively transitioning to 64-bit, even on mobile. The remaining space for 32-bit seems ever shrinking. Yet, it’s still present, in more places than can be listed. For example, many virtual environment generate bytecodes designed to produce a 32-bit application.
Thing is, most modern hash algorithms take advantage of 64-bit instructions, which can ingest data twice faster, so it’s key to great speed. Once translated for the 32-bit world, these 64-bit instructions can still be emulated, but at a cost. In most cases, it translates into a massive speed loss. That’s why XXH32 remains popular for 32-bit applications, it’s a great performer in this category.
A nice property of XXH3 is that it doesn’t lose so much speed when translated into 32-bit instructions. This is due to some careful choices in instructions used in the main loop. The result is actually pretty good :

XXH3 can overtake XXH32, even without vectorial instruction ! Enabling SSE2 put it in another league.
A similar property can be observed on ARM 32-bit. The base speed is very competitive, and the NEON vectorial code path designed by Devin makes wonder, pushing speed to new boundaries.
Hashing small inputs
The high speed achieved on large input wasn’t actually the center of my investigation.
The main focus is about short keys of random lengths, with a distribution of length roughly in the 20-30 bytes area, featuring occasional outliers, both tiny and large.
This scenario is very different. Actually, with such small input, the vectorized inner loop is never triggered. Delivering a good quality hash result must be achieved using a small amount of operations.
This investigation quickly converged onto Google’s CityHash, by Geoff Pyke and Jyrki Alakuijala. This algorithm features an excellent access pattern for small data, later replicated into FarmHash, giving them an edge. This proved another major source of inspiration for XXH3.
A small concern is that Cityhash comes in 2 variants, with or without seed. One could logically expect that both variants are “equivalent”, with one just setting a default seed value.
That’s not the case. The variant without seed forego the final avalanche stage, making it faster. Unfortunately, it also makes it fail SMHasher’s avalanche test, showing very large bias. For this reason, I will distinguish both variants in the graph, as the speed difference on small inputs is quite noticeable.
The benchmark test looks simple enough : just loop over some small input of known size, and count the nb of hashes produced. Size is only known at run time, so there’s no way for the compiler to “specialize” the code for a given size. There are some finicky details in ensuring proper timing, but once solved, it gives an interesting ranking.

Top algorithms are based on the same “access pattern”, and there are visible “steps” on reaching 33+ length, and then again at 65+. That’s because, in order to generate less branches, the algorithm does exactly the same work from 33 to 64 bytes. So the amount of instructions to run is comparatively large for 33 bytes.
In spite of this, XXH3 maintains a comfortable lead even at “bad” length values (17, 33, 65).
This first results looks good, but it’s not yet satisfying.
Remember the “variable size” requirement ?
This is not met by this scenario.
Impact of variable input sizes
Always providing the same input size is simply too easy for branches. The branch predictor can make a good job at guessing the outcome every time.
This is just not representative of most real-life scenarios, where there’s no such predictability. Mix inputs of different sizes, and it wreaks havoc on all these branches, adding a considerable cost at each hash. This impact is often overlooked, because measuring it is a bit more difficult. But it’s important enough to deserve some focus.
In the following scenario, input sizes are presumed randomly distributed between 1 and N. The distribution of lengths is pre-generated, and the same distribution is used for all hashes for a same N. This lean towards worst case scenario: generally, input sizes feature some kind of locality (as in target scenario, mostly between 20 and 30 bytes). But it gives us a good idea of how algorithms handle varying sizes.

This is a more significant victory for algorithms with an optimized access pattern. When input sizes become unpredictable, branch mispredictions become a much larger contributor to performance. The optimized access pattern makes the workload more predictable, and reduces the nb of branches which can be mispredicted. This is key to preserve a good level of performance in these conditions.
Throughput versus Latency
Throughput is relatively simple to measure : just loop over a bunch of inputs, hash them, then count the number of hashes completed in a given time.
But one could wonder if throughput is an appropriate metric. It represents a “batch” workload, where a ton of hashes are feverishly completed one after another. It may happen sometimes.
But in many cases, hashing is just one operation sandwiched between other very different tasks. This is a completely different background.
In this new setup, hashing must wait for prior operation to complete in order to receive its input, and later operation is blocked as long as the hash result is not produced. Hence latency seems a much better metric.
However, measuring latency is a lot more complex. I had many false starts in this experiment.
I initially thought that it would be enough to provide the result of previous hash as seed of the next hash. It doesn’t work : not only some algorithms do not take seed as arguments, a few others only use the seed at the very end of the calculation, letting them start hash calculations before the end of previous hash.
In reality, in a latency scenario, the hash is waiting for the input to be available, so it’s the input which must be based on previous hash result. After a lot of pain, the better solution was finally suggested by Felix Handte : use a pre-generated buffer of random bytes, and start hashing from a variable position derived from previous hash result. It enforces that next hash has to wait for previous hash result before starting.
This new setup creates a surprisingly different ranking :
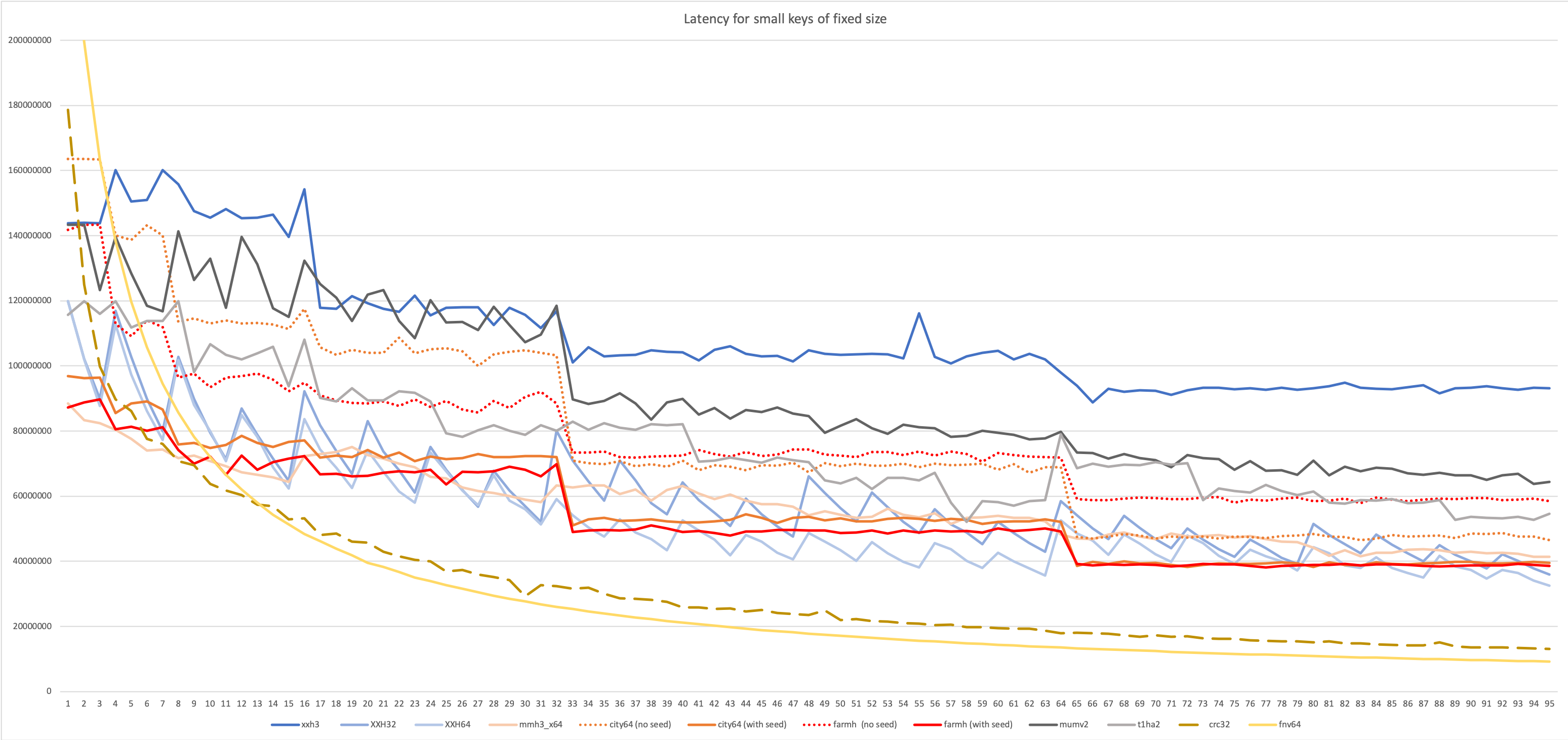
Measurements are a bit noisy, but trends look visible.
The latency-oriented test favors algorithms like Vladimir Makarov’s mumv2 and Leo Yuriev’s t1ha2, using the 64x64=>128-bits multiplication. This proved another source of inspiration for XXH3.
Cityhash suffers in this benchmark. Cityhash is based on simpler instructions, and completing a hash requires many more of them. In a throughput scenario, where there is no serialization constraint, Cityhash can start next hash before finishing previous one. Its simple instructions can be spread more effectively over multiple execution units, achieving a high level of IPC (Instruction per Clock). This makes Cityhash throughput friendly.
In contrast, the 64x64=>128-bits multiplication has access to a very restricted set of ports, but is more powerful at mixing bits, allowing usage of less instructions to create a hash with good avalanche properties. Less instructions translate into a shorter pipeline.
In the latency scenario, mumh2 fares very well, fighting for first place up to the 32-byte mark, after which XXH3 starts to take a lead.
However, this scenario involves fixed input size. It’s simple to code and explain, but as we’ve seen before, fixed size is actually an uncommon scenario : for most real-world use cases, input has an unpredictable size.
Hence, let’s combine the benchmark techniques seen previously, and look at the impact of random input lengths on latency.
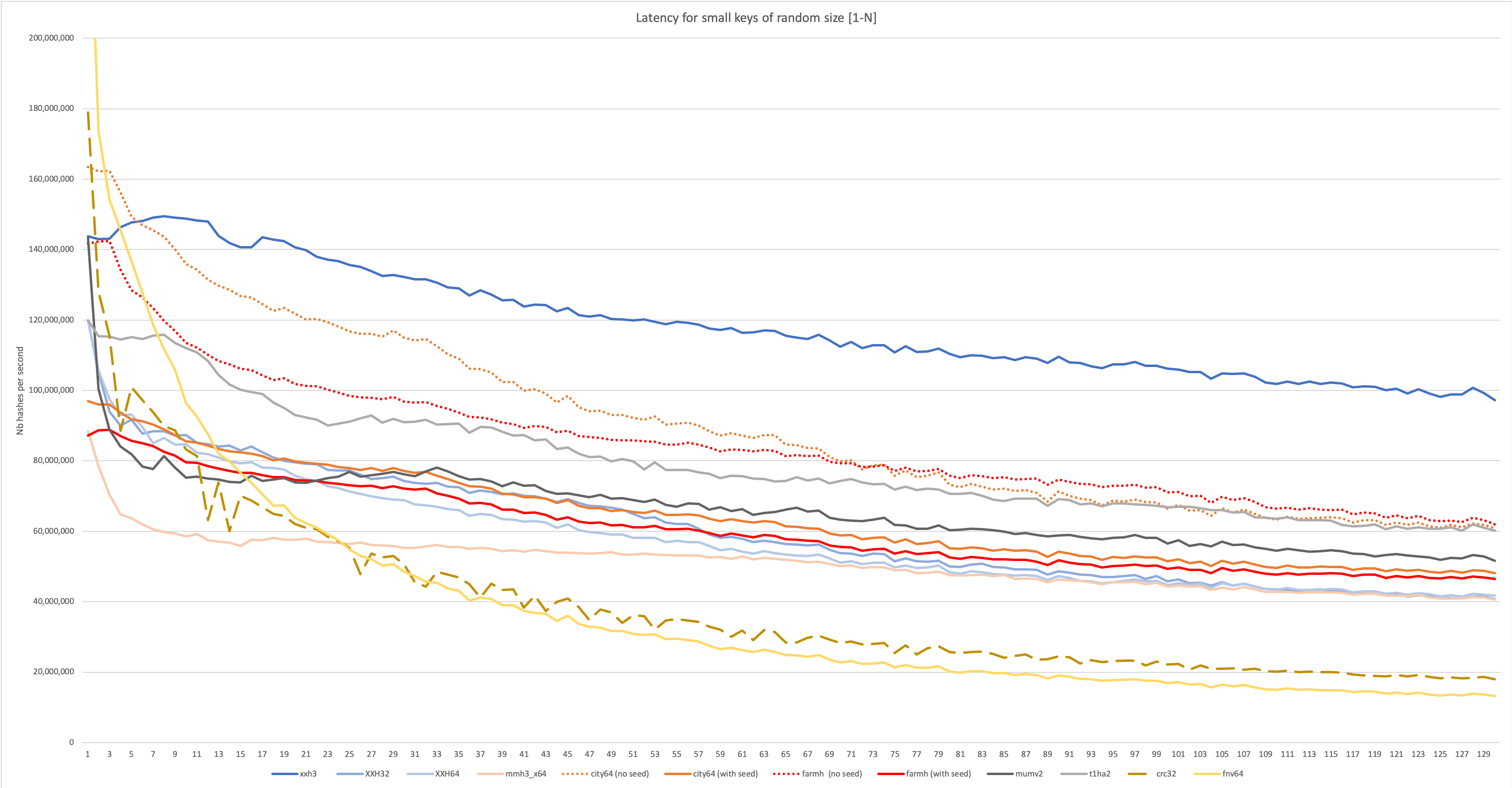
This is an important graph, as it matches the target use case of XXH3, and incidentally many real-world database/server use cases I’m aware of.
The variable size scenario favors algorithms using an optimized access pattern to reduce branch misprediction. mumv2, which was performing very well when input size was stable, loses a lot in this scenario. t1ha2 makes a better effort, and while not as well optimized as Cityhash for this purpose, loses nonetheless much less performance to variable input size, overtaking second place (if one does not count the “seed-less” variants in the ranking, due to afore-mentioned avalanche problems).
As could be expected, XXH3 is well tuned for this scenario. It’s no surprise since it was its target. So it’s basically mission accomplished ?
Hash Quality
It wouldn’t be a complete presentation without a note on hash quality. A good hash should make collisions as rare as possible, bounded by the birthday paradox, and offer great avalanche property : two different inputs shall produce vastly different output, even if they only differ by a single bit.
As expected, XXH3 completes all tests from SMHasher test suite. Both 64 and 128-bit variants were validated, as well as each of their 32-bit constituent.
But it went a bit farther.
SMHasher was designed many years ago, at a time when hashing was mostly a single main loop iterating over input. But as hash algorithms have become more powerful, this model feels no longer correct : modern hashes tend to feature a large inner loop, which is only triggered after a certain length. That means that the algorithm being tested when there are only a few input bytes is actually different from the one run on large inputs.
Because search space tends to explode with input size, and because computing capacity used to be weaker when SMHasher was created, most tests are concentrated on small inputs. As a consequence, tests for larger input sizes are very limited.
In order to stress the algorithm, it was necessary to push the tests beyond their usual limits. So I created a fork of rurban’s excellent SMHasher fork, methodically increasing limits to new boundaries. It’s still the same set of tests, but exploring a larger space, hence longer to run.
This proved useful during the design stage, eliminating risks of long-distance “echo” for example (when bits cancel each other by virtue of being at some exact relative position).
It also proved interesting to run these extended tests on existing algorithms, uncovering some “surprises” that were masked by the lower threshold of original tests.
To this end, these changes will be offered back to rurban’s fork, in the hope that they will prove useful for future testers and implementers.
Release
XXH3 is now released as part of xxHash v0.7.0. It’s still labelled “experimental”, and must be unlocked using macro XXH_STATIC_LINKING_ONLY. It’s suitable for ephemeral data and tests, but avoid storing long-term hash values yet. This period will be used to gather user’s feedback, after which the algorithm will transferred into stable in a future release.
Update: Since the release of xxHash v0.8.0, XXH3 is now labelled "stable", meaning produced hash values can be stored on disk or exchanged over a network, as any future version is now guaranteed produce the same hash value. Compared with initial release, v0.8.0 comes with streaming capabilities, 128-bit variant support, and better inlining.